高考中的立体几何问题(文科数学全国1卷)
马丽丽
立体几何作为高考中的一大板块,其重要程度是不言而喻的。为了对立体几何进行更有针对性、更有效的复习,我对近五年文科数学全国1卷中的立体几何题做了深入的研究。
一、试卷分析
经过分析归纳总结,我绘制了如下表格:
|
题号 |
分值 |
总分值 |
几何 背景 |
考点 |
2018全国卷1 |
5 |
5 |
27 |
圆柱 |
轴截面,表面积 |
9 |
5 |
圆柱 |
已知三视图,还原几何体,圆柱侧面展开图 |
10 |
5 |
长方体 |
线面角,长方体体积 |
18 |
12 |
折叠问题 |
折叠问题,面面垂直,三棱锥体积 |
2017全国新课标卷1 |
6 |
5 |
22 |
正方体 |
线面平行 |
16 |
5 |
三棱锥 |
三棱锥外接球的表面积,面面垂直 |
18 |
12 |
四棱锥 |
面面垂直,四棱锥体积,四棱锥表面积 |
2016全国新课标卷1 |
7 |
5 |
22 |
简单组合体(挖去体) |
三视图,球的体积,球的表面积 |
11 |
5 |
正方体 |
线面平行,空间两直线所成的角 |
18 |
12 |
正三棱锥 |
正投影,线面垂直,线线垂直,四面体的体积 |
2015全国新课标卷1 |
6 |
5 |
22 |
圆锥 |
数学文化,圆锥的体积 |
11 |
5 |
简单组合体(拼接体) |
三视图,表面积 |
18 |
12 |
四棱锥 |
线面垂直,面面垂直,三棱锥的体积,三棱锥的侧面积 |
2014全国新课标卷1 |
8 |
5 |
17 |
三棱柱 |
已知三视图,还原几何图 |
19 |
12 |
三棱柱 |
线面垂直,线线垂直,三棱柱的高 |
从上述表格中我们可以看到,立体几何在高考中所占的分值平均为22分(两个小题,一个大题),2018年甚至达到了27分,所以教学中一定要重视立体几何的复习以及得分。
二、考情考点分析
1)空间几何体的结构、三视图、直观图。
空间几何体的结构特征、三视图、直观图在高考中几乎年年考查。主要考查根据几何体的三视图求其体积与表面积,或者与立体几何的其他知识相结合,要求学生具有较强的空间想象能力。以选择题和填空题为主。
2)空间几何体的表面积与体积。
表面积与体积是高考考查的重点内容,主要考查空间几何体的表面积与体积的计算,涉及空间几何体的结构特征、三视图等内容,要求学生有较强的空间想象能力和计算能力,经常应用转化与化归思想。选择题、填空题和解答题都有考到。
3)空间点、直线、平面之间的位置关系。
主要考查与点、线、面位置关系有关的命题的真假判断和求解异面直线所成的角,要求有较强的空间想象能力和逻辑推理能力,以选择题和填空题为主。
4)直线、平面平行、垂直的判定与性质。
该部分是高考重点考查内容,涉及线线平行、线面平行、面面平行、线线垂直、线面垂直、面面垂直的判定及其性质,及其灵活应用。要求有较强的推理论证能力,广泛应用转化与化归思想,以解答题为主,小题也有涉及。
 三、典型高考题解析
三、典型高考题解析
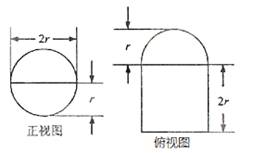
例1(2015全国新课标卷1第11题)圆柱被一个平面截去一部分后与半球(半径为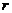 )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为
)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为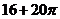 ,则
,则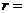 ( )
( )
(A)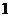 (B)
(B)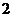
(C)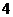 (D)
(D)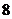
思路探求:由正视图和俯视图可知,该几何体是半球与半个圆柱的组合体,圆柱的底面半径与球的半径都为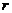 ,圆柱的高为
,圆柱的高为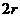 ,其表面积为
,其表面积为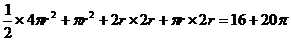 ,解得
,解得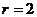
解答:选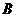
方法点睛:空间几何体的结构特征、三视图、直观图在高考中几乎年年考查,经常与表面积和体积结合考查,主要考查常见几何体及其组合体的三视图。
例2(2017全国新课标卷1第16题)已知三棱锥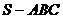 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上,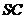 是球
是球 的直径。若平面
的直径。若平面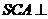 平面
平面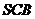 ,
,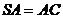 ,
,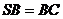 ,三棱锥
,三棱锥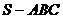 的体积为9,则球
的体积为9,则球 的表面积为________。
的表面积为________。
思路探求:取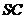 的中点
的中点 ,连接
,连接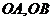 .因为
.因为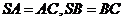 ,所以
,所以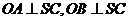 .因为平面
.因为平面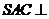 平面
平面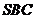 ,所以
,所以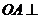 平面
平面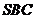 .设
.设 ,则
,则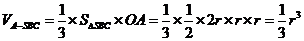 ,所以
,所以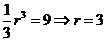 ,所以球的表面积为
,所以球的表面积为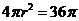
解答: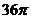
方法点睛:本题考查三棱锥的外接球。与求有关的切接问题关键是要找到(或设出)球心,然后利用球面上点到球心的距离为半径,通过作截面、补形、解方程等方法将半径求出。
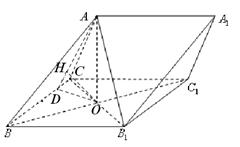
 例3(2014全国新课标卷1第19题) 如图,三棱柱
例3(2014全国新课标卷1第19题) 如图,三棱柱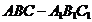 中,侧面
中,侧面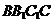 为菱形,
为菱形,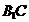 的中点为
的中点为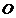 ,且
,且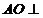 平面
平面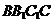 .
.
(I)证明: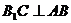
(II)若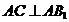 ,
,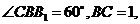 求三棱柱
求三棱柱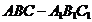 的高.
的高.
思路探求:(I)要证明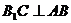 ,我们可以通过面面垂直来证明线面垂直,经分析
,我们可以通过面面垂直来证明线面垂直,经分析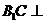 平面
平面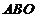 .
.
(II)求三棱柱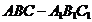 的高,可以直接将高作出来,但技巧性较强。也可以通过等体积法把问题转化。
的高,可以直接将高作出来,但技巧性较强。也可以通过等体积法把问题转化。
解答:(I)连结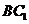 ,则
,则 为
为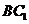 与
与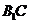 的交点,因为侧面
的交点,因为侧面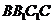 为菱形,所以
为菱形,所以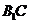
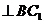 ,又
,又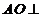 平面
平面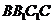 ,故
,故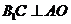 ,所以
,所以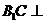 平面
平面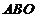 ,由于
,由于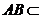 平面
平面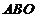 , 故
, 故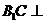

(II)解法1:作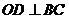 ,垂足为
,垂足为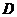 ,连结
,连结 ,作
,作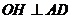 ,垂足为
,垂足为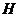 ,
,
 因为
因为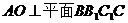 ,故
,故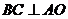 ,又因为
,又因为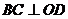 ,所以
,所以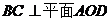 ,所以
,所以 .又
.又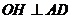 ,所以
,所以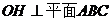 .因为
.因为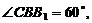 所以△
所以△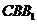 为等边三角形,故在
为等边三角形,故在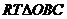 中,
中,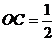 ,
,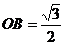 ,
,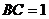 ,可得
,可得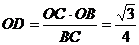 ,由于
,由于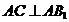 ,所以
,所以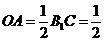 ,在
,在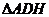 中,
中,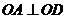 ,
,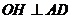 ,故
,故 ,且
,且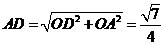 ,得
,得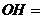
 .
.
又因为 为
为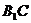 的中点,所以点
的中点,所以点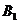 到平面
到平面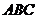 的距离为
的距离为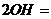
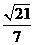 ,故三棱柱
,故三棱柱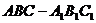 的高为
的高为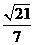 .
.
解法2:三棱柱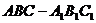 的高即为三棱锥
的高即为三棱锥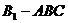 的高,设其为
的高,设其为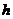 .因为
.因为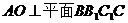 ,所以
,所以 ,即
,即 .同解法1过程,可求得
.同解法1过程,可求得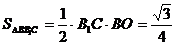 ,
,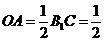 ,
,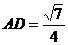
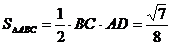 .故
.故 .
.
方法点睛:线、面平行、垂直位置关系是高考考查的重点内容,要熟练掌握平面几何中的平行、垂直的相关结论,以及高中阶段学习的线、面平行、垂直的判定定理和性质,方能在解题时实现线线平行、线面平行、面面平行、线线垂直、线面垂直、面面垂直的灵活转化。求三棱柱的高时,除了可以考虑把高作出来,也可以灵活转化,利用三棱锥的等体积法是求高的重要方法。另外,空间几何体的表面积和体积也是考查的重点,如2015全国新课标卷1第18题,2016全国新课标卷1第18题,2017全国新课标卷1第18题,2018全国新课标卷1第18题。

